Bayesian Multiple Regression

We can replace normal multiple regression with Bayesian Multiple Regression.

Model and Data

First, we need to create simulation data. Let’s consider this model:

\(\newcommand{\Normal}{\mathcal{N}} \newcommand{\Ga}{\rm Gamma} \begin{align} y_i &\sim \Normal(\beta_0 + \beta_1 x_{1i} + \beta_2 x_{2i},\ 1/ \tau ) \\ \beta_0 &\sim \Normal (\mu_0,\ 1/ \tau_0 ) \\ \beta_1 &\sim \Normal (\mu_1,\ 1/ \tau_1 ) \\ \beta_2 &\sim \Normal (\mu_2,\ 1/ \tau_2 )\\ \tau &\sim \Ga (\alpha, \beta) \end{align}\)

Generate data with R:

num_data <- 1000
N <- num_data

age <- rnorm(num_data, mean=50, sd=15)
income <- rnorm(num_data, mean=500, sd=100) # using Normal might be wrong, but just for simulation data
data <- data.frame(age, income)
covariates <- as.matrix(data[,c("age", "income")])


## Muliple Regression
true_beta0 <- 1.5
true_beta1 <- 2.8
true_beta2 <- -1.2
tau_true <- 1
betaX <- c(true_beta1, true_beta2)
data$Y <- true_beta0 + covariates %*% betaX + rnorm(num_data, sd=1/sqrt(tau_true))

Likelihood function

Likelihood function is simple:

\(\newcommand{\Normal}{\mathcal{N}} \begin{align} \mathcal{L} = \prod_{i=1}^N \Normal(\beta_0 + \beta_1 x_{1i} + \beta_2 x_{2i},\ 1/ \tau ) \end{align}\)

Update Equations

Update for \(\beta_0\) (intercept)

\(\newcommand{\Normal}{\mathcal{N}} \begin{align} &p(\beta_0 | \beta_1,\beta_2, \tau, y, x, \mu_0,\mu_1,\mu_2 \tau_0,\tau_1,\tau_2,\alpha,\beta)\\ &\propto p(\beta_0 , \beta_1,\beta_2, \tau, y, x, \mu_0,\mu_1,\mu_2 \tau_0,\tau_1,\tau_2,\alpha,\beta)\\ &= p(y|\beta_0,\beta_1,\beta_2,\tau,x)\ p(\beta_0|\mu_0,\tau_0)\ p(\beta_1|\mu_1,\tau_1)\ p(\beta_2|\mu_2,\tau_2)\ p(x) \\ &\propto p(y|\beta_0, \beta_1, \beta_2, \tau, x)\ p(\beta_0 | \mu_0, \tau_0)\\ &= \Normal(\mu_0,\ 1/\tau_0)\ \prod_{i=1}^N (\beta_0 + \beta_1 x_{1i} + \beta_2 x_{2i},\ 1/ \tau) \\[10pt] &= -\frac{1}{2} \log \left(2 \pi \cdot \frac{1}{\tau_0} \right) - \frac{\tau_0 (\beta_0 - \mu_0)^2}{2} + \sum_{i=1}^{N} - \left( \frac{1}{2} \log \left(2 \pi \cdot \frac{1}{\tau} \right) + \frac{\tau(y_i - \beta_0 - \beta_1 x_{1i} - \beta_2 x_{2i})^2}{2} \right)\\ &\propto - \frac{\tau_0 (\beta_0 - \mu_0)^2}{2} - \frac{\tau}{2} \sum_{i=1}^N (y_i - \beta_0 - \beta_1 x_{1i} - \beta_2 x_{2i})^2 \ \ \ \cdots\cdots (1) \end{align}\)

Note that \(p(y|\beta_0, \beta_1, \beta_2, \tau, x)\) and \(p(\beta_0 | \mu_0, \tau_0)\) are Normal distribution, so we can rewrite them. Also, log Normal PDF is important in deriving.

\(\begin{align} -\frac{1}{2} \log (2 \pi \sigma^2) - \frac{(x - \mu)^2}{2 \sigma^2} = -\frac{1}{2} \log \left( \frac{2 \pi}{\tau} \right) - \frac{\tau(x - \mu)^2}{2} \end{align}\)

Another important and useful property of Normal distribution is that, when we focus on \(x\),

\(\newcommand{\Normal}{\mathcal{N}} \begin{align} &{\rm if}\ \ x \sim \Normal(u,\ 1/t),\\ &-\frac{t}{2} (x - u)^2 \propto - \frac{t}{2} x^2 + tux \ \ \ \cdots\cdots (2) \end{align}\)

Also, remember \((x + y + z + w)^2 = (y + (x + z + w))^2\). Now, let’s resume (1).

\(\newcommand{\Normal}{\mathcal{N}} \begin{align} (1) &\propto - \frac{\tau_0}{2} \beta_0^2 + \tau_0 \mu_0 \beta_0 - \frac{\tau}{2} \sum_{i=1}^N \left(\beta_0^2 - 2 \beta_0 (y_i - \beta_1 x_{1i} - \beta_2 x_{2i}) \right) \ \ \ \cdots\cdots (3) \\ &= - \frac{\tau_0}{2} \beta_0^2 + \tau_0 \mu_0 \beta_0 - \frac{\tau}{2} N \beta_0^2 + \tau \sum_{i=i}^N \beta_0 (y_i - \beta_1 x_{1i} - \beta_2 x_{2i}) \\ &= \left( - \frac{\tau_0 + \tau N}{2} \right) \beta_0^2 + \left( \tau_0 + \tau N \right) \left( \frac{\tau_0}{\tau_0 + \tau N} \right) \mu_0 \beta_0 + \left( \tau_0 + \tau N \right) \left( \frac{\tau}{\tau_0 + \tau N} \right) \beta_0 \sum_{i=1}^N (y_i - \beta_1 x_{1i} - \beta_2 x_{2i})\\ &= \left( - \frac{\tau_0 + \tau N}{2} \right) \beta_0^2 + (\tau_0 + \tau N) \cdot \left( \frac{\tau_0 \mu_0 + \tau \sum_N (y_i - \beta_1 x_{1i} - \beta_2 x_{2i})}{\tau_0 + \tau N} \right) \cdot \beta_0 \end{align}\)

By comparing the last equation with (2), we can say

\(\newcommand{\Normal}{\mathcal{N}} \begin{align} p(\beta_0 | \beta_1,\beta_2, \tau, y, x, \mu_0,\mu_1,\mu_2 \tau_0,\tau_1,\tau_2,\alpha,\beta) \sim \Normal \left( \frac{\tau_0 \mu_0 + \tau \sum_N (y_i - \beta_1 x_{1i} - \beta_2 x_{2i})}{\tau_0 + \tau N} ,\ 1/(\tau_0 + \tau N) \right) \end{align}\)

# beta_0
sample_beta_0 <- function(y, x1, x2, beta_1, beta_2, tau, mu_0, tau_0){
  precision <- tau_0 + tau * N
  mu <- tau_0 * mu_0 + tau * sum(y - (beta_1 * x1) - (beta_2 * x2))
  mu <- mu / precision
  value <- rnorm(1, mean=mu, sd=1/sqrt(precision))
  return(value)
}

Update for \(\beta_1\) (coefficient)

Derivation is quite similar until (1). We have slightly different form for (3) because we now focus on \(\beta_1\).

\(\newcommand{\Normal}{\mathcal{N}} \begin{align} &p(\beta_1 | \beta_0,\beta_2, \tau, y, x, \mu_0,\mu_1,\mu_2 \tau_0,\tau_1,\tau_2,\alpha,\beta)\\ &\propto - \frac{\tau_1}{2} \beta_1^2 + \tau_1 \mu_1 \beta_1 - \frac{\tau}{2} \sum_{i=1}^N \left( \beta_1^2 x_{1i}^2 - 2 \beta_1 x_{1i}^2 (y_i - \beta_0 - \beta_2 x_{2i}) \right) \\ &= \left( - \frac{\tau_1 + \tau \sum_N x_{i1}^2}{2} \right) \beta_1^2 + \tau_1 \mu_1 \beta_1 + \tau \sum_{i=1}^2 \left( \beta_1 x_{i1} (y_i - \beta_0 - \beta_2 x_{2i}) \right) \\ &= \left( - \frac{\tau_1 + \tau \sum_N x_{i1}^2}{2} \right) \beta_1^2 + \left[ \tau_1 \mu_1 + \tau \sum_{i=1}^N x_{1i} (y_i - \beta_0 - \beta_2 x_{2i}) \right] \beta_1\\ &= \left( - \frac{\tau_1 + \tau \sum_N x_{i1}^2}{2} \right) \beta_1^2 + (\tau_1 + \tau \sum_N x_{i1}^2) \frac{ \tau_1 \mu_1 + \tau \sum_{i=1}^N x_{1i} (y_i - \beta_0 - \beta_2 x_{2i}) }{\tau_1 + \tau \sum_N x_{i1}^2} \beta_1 \end{align}\)

Now, we get

\(\newcommand{\Normal}{\mathcal{N}} \begin{align} p(\beta_1 | \beta_0,\beta_2, \tau, y, x, \mu_0,\mu_1,\mu_2 \tau_0,\tau_1,\tau_2,\alpha,\beta) \sim \Normal \left( \frac{\tau_1 \mu_1 + \tau \sum_N x_{1i} (y_i - \beta_0 - \beta_2 x_{2i})}{\tau_1 + \tau \sum_N x_{1i}^2} ,\ 1/(\tau_1 + \tau \sum_N x_{1i}^2) \right) \end{align}\)

# beta_1
sample_beta_1 <- function(y, x1, x2, beta_0, beta_2, tau, mu_1, tau_1){
  precision <- tau_1 + tau * sum(x1*x1)
  mu <- tau_1 * mu_1 + tau * sum(x1 * (y - beta_0 - beta_2 * x2))
  mu <- mu / precision
  value <- rnorm(1, mean=mu, sd=1/sqrt(precision))
  return(value)
}

We can get the similar equation for \(\beta_2\).

# beta_2
sample_beta_2 <- function(y, x1, x2, beta_0, beta_1, tau, mu_2, tau_2){
  precision <- tau_2 + tau * sum(x2*x2)
  mu <- tau_2 * mu_2 + tau * sum(x2 * (y - beta_0 - beta_1 * x1))
  mu <- mu / precision
  value <- rnorm(1, mean=mu, sd=1/sqrt(precision))
  return(value)
}

Update for \(\tau\) (precision)

Let’s recall log PDF of Gamma distribution:

\(\begin{align} \log \frac{\beta^\alpha}{\Gamma (\alpha)} + (\alpha-1) \log x - \beta x \propto (\alpha - 1) \log x - \beta x \end{align}\)

We can get updat equation:

\(\newcommand{\Normal}{\mathcal{N}} \begin{align} &p( \tau | \beta_0, \beta_1, \beta_2, y, x, \mu_0,\mu_1,\mu_2 \tau_0,\tau_1,\tau_2,\alpha,\beta) \\ &\propto p(y | \beta_0, \beta_1, \beta_2, \tau, x) p(\tau | \alpha, \beta)\\ &= \sum_{i=1}^N - \left( \frac{1}{2} \log \left(2 \pi \cdot \frac{1}{\tau} \right) + \frac{\tau}{2} (y_i - \beta_0 - \beta_{1} x_{1i} - \beta_2 x_{2i})^2 \right) + (\alpha - 1) \log \tau - \beta \tau\\ &= \sum_{i=1}^N - \left( \frac{1}{2} \left(\log 2 + \log \pi + \log \frac{1}{\tau} \right) + \frac{\tau}{2} (y_i - \beta_0 - \beta_{1} x_{1i} - \beta_2 x_{2i})^2 \right) + (\alpha - 1) \log \tau - \beta \tau\\ &\propto \sum_{i=1}^N - \left( \frac{1}{2} \left(\log \frac{1}{\tau} \right) + \frac{\tau}{2} (y_i - \beta_0 - \beta_{1} x_{1i} - \beta_2 x_{2i})^2 \right) + (\alpha - 1) \log \tau - \beta \tau\\ &= - \frac{N}{2} \log \frac{1}{\tau} - \frac{\tau}{2} \sum_{i=1}^N (y_i - \beta_0 - \beta_{1} x_{1i} - \beta_2 x_{2i})^2 + (\alpha - 1) \log \tau - \beta \tau\\ &= \frac{N}{2} \log \tau - \frac{\tau}{2} \sum_{i=1}^N (y_i - \beta_0 - \beta_{1} x_{1i} - \beta_2 x_{2i})^2 + (\alpha - 1) \log \tau - \beta \tau\\ &= \left( \alpha + \frac{N}{2} - 1 \right) \log \tau - \left( \beta + \sum_{i=1}^N \frac{(y_i - \beta_0 - \beta_{1} x_{1i} - \beta_2 x_{2i})^2}{2} \right) \tau \end{align}\)

So, we get \(\newcommand{\Normal}{\mathcal{N}} \begin{align} &p( \tau | \beta_0, \beta_1, \beta_2, y, x, \mu_0,\mu_1,\mu_2 \tau_0,\tau_1,\tau_2,\alpha,\beta) \sim {\rm Gamma} \left(\alpha + \frac{N}{2} , \ \beta + \sum_{i=1}^N \frac{(y_i - \beta_0 - \beta_{1} x_{1i} - \beta_2 x_{2i})^2}{2} \right) \end{align}\)

# tau
sample_tau <- function(y, x1, x2, beta_0, beta_1, beta_2, alpha, beta){
  alpha_new <- alpha + N/2
  resid <- y - beta_0 - (beta_1 * x1) - (beta_2 * x2)
  beta_new <- beta + sum(resid*resid) / 2
  value <- rgamma(1, shape=alpha_new, rate=beta_new)
    # alpha = shape, beta = 1/rate in rgamma()
}

Sampling

iter_num <- 15000

# Prepare storages
beta_0 <- rep(NA, iter_num)
beta_1 <- rep(NA, iter_num)
beta_2 <- rep(NA, iter_num)
tau <- rep(NA, iter_num)

# Initialization
beta_0[1] <- 0
beta_1[1] <- 1
beta_2[1] <- 2
tau[1] <- 2
# Run
for(i in 1:(iter_num-1)){
  beta_0[i+1] <- sample_beta_0(data$Y, data$age, data$income, beta_1[i], beta_2[i], tau[i], 0, 0.01)
  beta_1[i+1] <- sample_beta_1(data$Y, data$age, data$income, beta_0[i+1], beta_2[i], tau[i], 0, 0.01)
  beta_2[i+1] <- sample_beta_2(data$Y, data$age, data$income, beta_0[i+1], beta_1[i], tau[i], 0, 0.01)
  tau[i+1] <- sample_tau(data$Y, data$age, data$income, beta_0[i+1], beta_1[i+1], beta_2[i+1], alpha=2, beta=1)
}

Result

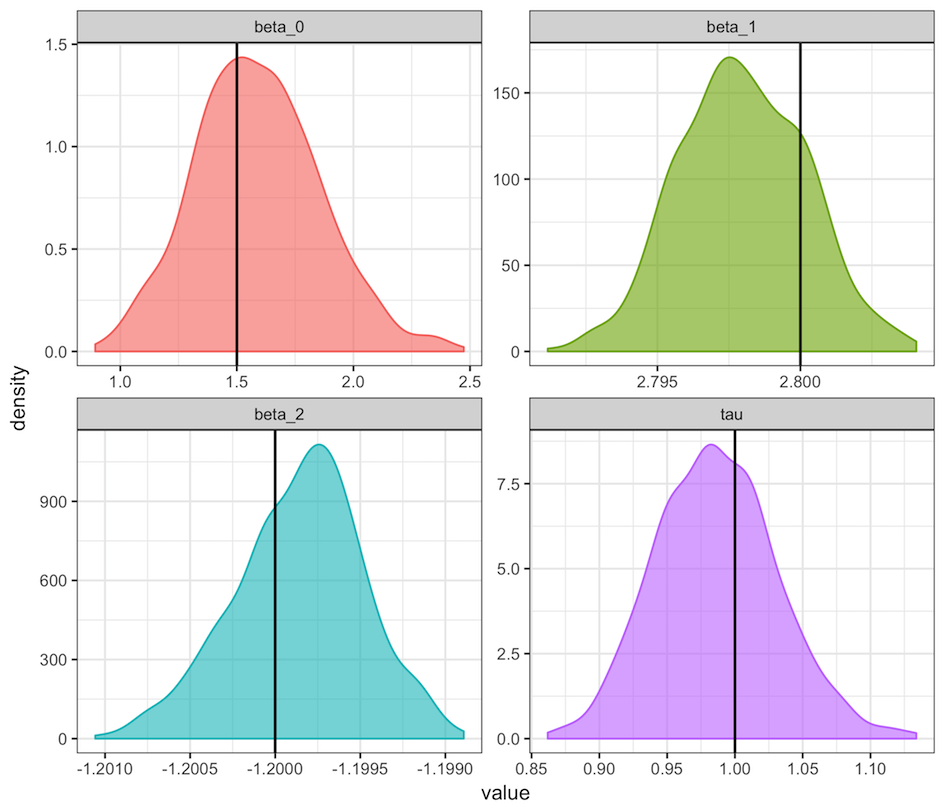
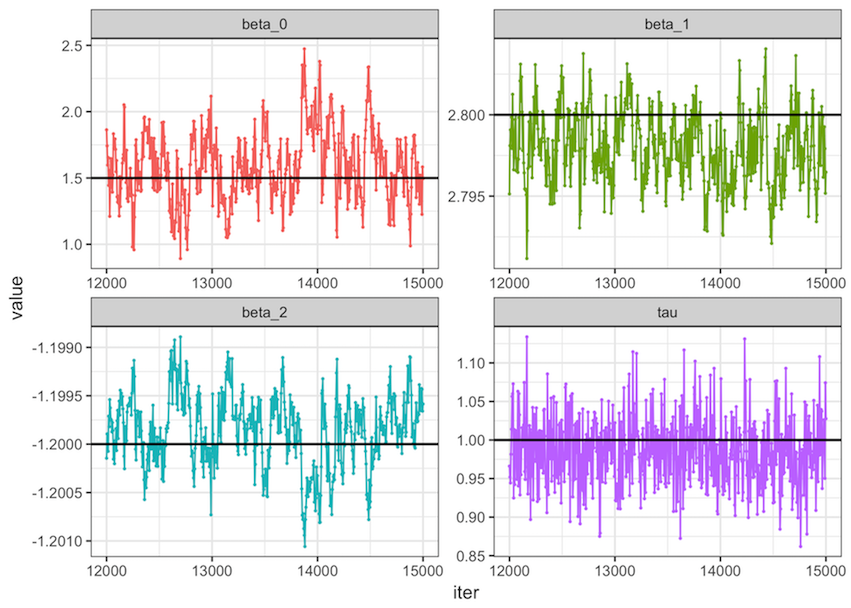
Code

# Set working directory
setwd("/Users/Study/Analysis/")

# Load library
library(tidyverse)
###############################################
# Bayesian Linear Regression (Gibbs Sampling) #
###############################################
iter_num <- 15000
burn_in_num <- 12000

####################
# Create fake data #
####################
num_data <- 1000
N <- num_data

age <- rnorm(num_data, mean=50, sd=15)
income <- rnorm(num_data, mean=500, sd=100)
data <- data.frame(age, income)
covariates <- as.matrix(data[,c("age", "income")])


## Multiple Regression
true_beta0 <- 1.5
true_beta1 <- 2.8
true_beta2 <- -1.2
tau_true <- 1
betaX <- c(true_beta1, true_beta2)
data$Y <- true_beta0 + covariates %*% betaX + rnorm(num_data, sd=1/sqrt(tau_true))


## Check with package
res_lm <- lm(Y ~ age + income, data)
summary(res_lm)

#############
# Inference #
#############
sample_beta_0 <- function(y, x1, x2, beta_1, beta_2, tau, mu_0, tau_0){
  precision <- tau_0 + tau * N
  mu <- tau_0 * mu_0 + tau * sum(y - (beta_1 * x1) - (beta_2 * x2))
  mu <- mu / precision
  value <- rnorm(1, mean=mu, sd=1/sqrt(precision))
  return(value)
}


sample_beta_1 <- function(y, x1, x2, beta_0, beta_2, tau, mu_1, tau_1){
  precision <- tau_1 + tau * sum(x1*x1)
  mu <- tau_1 * mu_1 + tau * sum(x1 * (y - beta_0 - beta_2 * x2))
  mu <- mu / precision
  value <- rnorm(1, mean=mu, sd=1/sqrt(precision))
  return(value)
}

sample_beta_2 <- function(y, x1, x2, beta_0, beta_1, tau, mu_2, tau_2){
  precision <- tau_2 + tau * sum(x2*x2)
  mu <- tau_2 * mu_2 + tau * sum(x2 * (y - beta_0 - beta_1 * x1))
  mu <- mu / precision
  value <- rnorm(1, mean=mu, sd=1/sqrt(precision))
  return(value)
}

sample_tau <- function(y, x1, x2, beta_0, beta_1, beta_2, alpha, beta){
  alpha_new <- alpha + N/2
  resid <- y - beta_0 - (beta_1 * x1) - (beta_2 * x2)
  beta_new <- beta + sum(resid*resid) / 2
  value <- rgamma(1, shape=alpha_new, rate=beta_new)
    # alpha = shape, beta = 1/rate
}

# Prepare storages
beta_0 <- rep(NA, iter_num)
beta_1 <- rep(NA, iter_num)
beta_2 <- rep(NA, iter_num)
tau <- rep(NA, iter_num)

# Initialization
beta_0[1] <- 0
beta_1[1] <- 1
beta_2[1] <- 2
tau[1] <- 2
# Run
for(i in 1:(iter_num-1)){
  beta_0[i+1] <- sample_beta_0(data$Y, data$age, data$income, beta_1[i], beta_2[i], tau[i], 0, 0.01)
  beta_1[i+1] <- sample_beta_1(data$Y, data$age, data$income, beta_0[i+1], beta_2[i], tau[i], 0, 0.01)
  beta_2[i+1] <- sample_beta_2(data$Y, data$age, data$income, beta_0[i+1], beta_1[i], tau[i], 0, 0.01)
  tau[i+1] <- sample_tau(data$Y, data$age, data$income, beta_0[i+1], beta_1[i+1], beta_2[i+1], alpha=2, beta=1)
}


# Make Figure
make_figure <- function(params, true_values, params_names, burn_in=2000, slice=5){
  num_params <- length(params)

  tidy_params <- list()
  for(i in 1:num_params){
    temp <- data.frame(value=params[[i]])
    temp$parameter <- params_names[i]
    temp$iter <- 1:nrow(temp)

    temp <- temp[burn_in:nrow(temp) ,]
    slice_index <- seq(1, nrow(temp), slice)# slice data
    temp <- temp[slice_index, ]
    tidy_params[[i]] <- temp
  }
  tidy_params <- do.call(rbind.data.frame, tidy_params)

  true <- data.frame(
    parameter = params_names,
    value = true_values
    )

  param <- ggplot(data=tidy_params, aes(x=iter, y=value, group=parameter, color=parameter)) + 
      geom_line() + 
      geom_point(size=0.3) +
      facet_wrap(~parameter, ncol=2, scales = "free") +
      geom_hline(data = true, aes(yintercept = value), size=0.7) +
      theme_bw() +
      theme(legend.position="none")

  param_density <- ggplot(data=tidy_params, aes(x=value, color=parameter, fill=parameter)) +
    geom_density(stat = "density", position = "identity",alpha=0.6) + 
    facet_wrap(~parameter, ncol=2, scales = "free") +
    geom_vline(data = true, aes(xintercept = value), size=0.7) +
    theme_bw() +
    theme(legend.position="none")

  return(list(param, param_density))

}

params <- list(beta_0, beta_1, beta_2, tau)
true_values <- c(true_beta0, true_beta1, true_beta2, tau_true)
params_names <- c("beta_0", "beta_1", "beta_2", "tau")
gs_res3 <- make_figure(params, true_values, params_names, burn_in=burn_in_num, slice=5)
gs_res3[[1]]
gs_res3[[2]]
saveRDS(gs_res3,"figure.obj")
saveRDS(data,"data.obj")
ggsave("trace.png", gs_res3[[1]], width=7, height=5)
ggsave("hist.png", gs_res3[[2]], width=7, height=6)